Back to index

Disjoint Sets

Operations

• union(S1, S2)
  • return union of $S_1$ and $S_2$
• find(S, x)
  • find the “representative member” (determined by some rule) of the set that $x$ belongs to

Let $\sigma$ be the procedure of $n - 1$ unions and $m \geq n$ finds

Naive implementations

Linked List

• one list per set
• for each list, store pointers to head and tail
  • this way, union is fast
• finding representative takes $\mathcal O(n)$ time

Augmented Linked List

• each element stores pointer to its representative
  • this way, find is fast
• union is slow because it must now change $\mathcal O(min(\vert S_1\vert , \vert S_2\vert ))$ pointers to the new representative

Forest (tree-like)

• each set is a tree
• root of a tree is representative of set
• non-root nodes point to a parent node
  • find works by ascending the tree until it reaches the root
  • it takes $\mathcal O(h)$ time where $h$ is height of tree
• union is fast because we must only change one parent pointer - make one tree’s root point to an element of other tree
  • to support this, record size (number of nodes) for each tree

Weighted Union

To do union, make root of smaller tree point to root of larger tree

Lemma

With weighted union, any tree $T$ of height $h$ created during the execution of $\sigma$ has $\vert T\vert \geq 2^h$

Proof.

Base case:

If $h = 0$, then the tree has $1 = 2^0$ node

Inductive step:

Suppose lemma holds for some $h \geq 0$.

To construct a tree of height $h+1$, we make the root of a tree $A$ of height $h$ point to the root of a bigger tree $B$ (because we are using weighted union)

By IH, $\vert A\vert \geq 2^h$

By WU rule, $\vert B\vert \geq \vert A\vert \geq 2^h$

Then resulting tree has number of nodes $\vert A\vert + \vert B\vert \geq 2 (2^h) = 2^{h + 1}$

Path compression

• find(S, x) ascends tree until root is reached
• intermediate nodes $n_1, …, n_m$ on way to root do not matter, so after we find root we can change n.parent = root for each $n$ on the way to the root (as well as x.parent = root

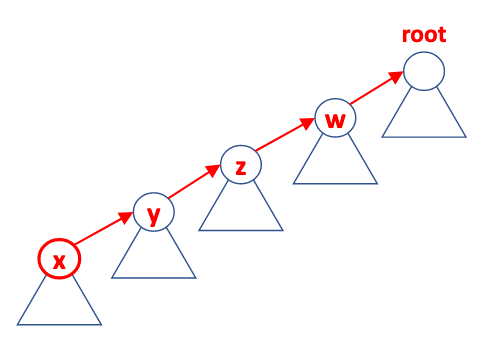
Before:

find(S, x) traverses from x to root

After:

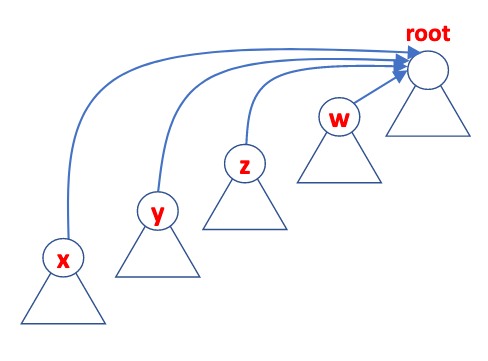
• this does not increase complexity, as same nodes must be operated on twice, aka a constant factor difference
• speeds up subsequent calls to find on x or any of its ancestors - becomes constant time
  • does not affect time for find on other parts of the tree, does not affect union at all

---

History: 25 years after publication of weighted union + path compression implementation, proof that $\sigma$ takes $\Theta(m \cdot \alpha(m, n))$ time using WU+PC was finally completed (where $\alpha$ is inverse Ackerman function).

The Ackerman function grows ridiculously quickly so $\alpha$ grows ridiculously slowly, so for all reasonable (read: physically possible) intents, $\sigma$ runs in linear time.

---